Transformer는 Decoder와 Encoder 구조로 이루어져 있다..! 앞에서 배운 핵심 개념들을 바탕으로 각 구조를 자세히 알아보도록 하자.
Transformer Decoder

쉽게 생각해서 Language models처럼 어떻게 우리가 systems을 build할까를 생각하면 된다.
minimal self-attention architecture로 보이지만, 사실 좀 더 많은 component가 있다!
- Embeddings와 Position Embeddings는 동일하다.
1. Multi-head Attention
먼저 self-attention이 아닌 multi-head self-attetion이네..?

여기서 알 수 있는 사실.. Head는 무엇을 attention 할 것인지를 결정해주는 것이라고 할 수 있다.
우선... Attention이 계산되는 과정을 알아보자!
Matrices에서 key-query-value attention이 어떻게 계산되는 지 봅시다...
- InputInput vectors의 concatenation라고 할 수 있다. X = [x1; ... ; xn] ∈ ℝ𝑛× 𝑑 (행이 n개, 열이 d개; 즉, n은 단어의 개수 d는 차원)
- Output
softmax(XQ(XK)T)XV ∈∈ℝ𝑛×𝑑
이때, 𝑋𝐾 ∈ ℝ𝑛×𝑑, 𝑋𝑄 ∈ ℝ𝑛×𝑑, 𝑋𝑉 ∈ ℝ𝑛×𝑑
1. Query-Key dot products : 𝑋𝑄 𝑋𝐾 ⊤
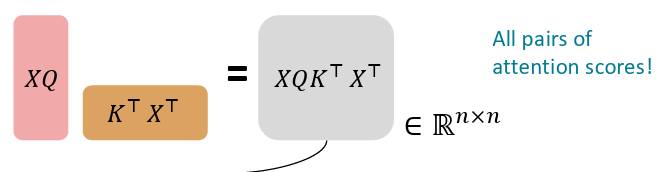
즉 결과는 쉽게 생각해서 각 Query 벡터와 각 Key 벡터 간의 dot product의 값을 모두 구한 matrix라고 보면 된다..!
결과 matrix의 (i,j)의 값은 Q의 i번째 행(i번째 word의 Query) K의 j번째 열(j번째 word의 Key)의 dot product (현재 Query가 Key를 얼마나 참고하는가?) 라고 보면 된다!! 그리고한 행이 Query에 대한 다른 key의 attention score가 된다.

그리고 softmax를 적용하먄,
각 행은 Query 위치 i가 전체 Key들(j=1~n)에 대해 attention하는 가중치
이를 V(각 word의 실제 정보)에 곱하여 weighted average를 계산한다!
softmax 결과의 한 행 (즉, Query가 보는 attention weight)
와 V의 한 열 (특정 의미 차원만 담고 있음)을 곱하면
과연 이게 무슨 의미지?”
Softmax한 한 행 × V의 한 열 =
"이 Query가 해당 의미 차원에 대해 얼마나 정보를 끌어왔는가?"
그리고 그걸 d_v 개 차원에 대해 모두 계산하니까
→ i번째 Query의 context vector가 나오는 거예요!
즉 결과 matrix의 (i, j)의 값은 한 word의 Attention 가중치에 대하여 다른 word들에 대해 곱하여 더한 값(이때 다른 word의 일부 차원만 곱한 것)
따라서 i번째 행은 전체 context임!!
만약 우리가 한 sentence에서 여러 위치를 한번에 보고싶다면 어떨까??
단어 i는 보통, self-attention이 xiTQTKxj (즉 xi의 Query, xj의 Key)가 높은 곳을 "보고"있는데, 즉 단어 j를 바라보는데, 어쩌면 다른 이유로 다른 j(다른 단어들)도 집중해서 보고 싶을 수도 있지 않을까?
우리는 여러 개의 Q, K, V metrices을 사용해서 여러 개의 attention "head"를 정의할 것이다.

Ql, Kl, Vl는 각각 l번째 head에서 사용되는 행렬이고,
h는 head의 개수, l은 head 번호 (1부터 h까지)라고 하자.
여기서 전체 차원 d를 head 수 h로 나누어서 각 head는 더 작고 독립적인 공간에서 작동함.

각 attention head는 attention은 독립적으로 수행한다.
attention score : XQl(Kl)TXT
value 합산 : 그 결과에

output vector를 행렬로 만든 후 combine
즉, 각 head는 서로 different things를 "보고", value vectors도 다르게 constrcut한다!!
효율적으로 계산하는 방법
우리가 h개의 많은 attention heads를 계산할지라도 그것은 매우 비싸지 않다.
1. 𝑋𝑄∈ℝ𝑛×𝑑 를 계산하고 ℝ𝑛×ℎ×𝑑/ℎ 로 reshape 한다. (XK, XV도 마찬가지로!!)
이렇게 되면 d차원의 n개의 word에서 attention head h개를 만들고 싶기 때문에
dimenstion d를 h개의 head로 나누고 각 head에 d/h만큼 할당해준다.
따라서 resahpe 시 각 단어(n)개가 h개의 head를 가지며 각 head는 d/h 차원의 query vector를 가진다. (2차원 행렬이었는데 이제 3차원 tensor가 된다)
2. ℝℎ×𝑛×𝑑/ℎ 로 transpose한다. 그러면 head axis이 batch axis처럼 작동한다. (또한 맨 앞이 보통 depth의 의미..!)
Transformer 구현에서는 각 head에 대해 독립적으로 attention을 계산해야 하는데, 보통 batch aixs를 제일 앞에 두고 batch 차원 단위로 병렬 연산을 수행한다.
즉, 각 head를 독립적인 sample처럼 병렬 처리 하기 위해서다!
그냥 쉽게 생각해서 h개의 head가 nxd/h의 크기의 matrix를 갖고 있다 생각하자!
원래:
[ 단어1: head1, head2, ..., headh ]
[ 단어2: head1, head2, ..., headh ]
↓
transpose
[ head1: 단어1, 단어2, ... ]
[ head2: 단어1, 단어2, ... ]
...
거의 다른 모든 것은 동일하고 행렬들의 크기들도 동일하다!!

위의 그림을 보면 head가 3인 것을 알 수 있다. (가로 세로가 차원과 대응되는게 아님 주의!!!)
XQ, XK: nxd/h가 3개 있다! 라고 이해하면 쉬울듯!
XQKX: 3개의 head가 각각 nxn 크기의 attention score matrix를 갖고 있다.
dot product해서 각 head의 attention score를 계산하게 된다.
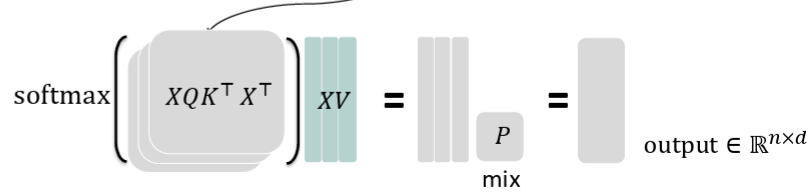
softmax를 수행한 후 각 head별로 weighted average 수행한다.
각 head의 attention scores matrix와 각 head의 XV를 각각 곱한 결과라고 생각하면 된다!
Scaled dot Product
Q와 K의 차원이 커지면 내적 값이 너무 커져서 softmax가 터지니까, 그걸 방지하려고 √(d/h)로 나눠주는 게 “Scaled Dot Product Attention”이다.
만약 dimensionality d (embedding 차원의 수)가 너무 커지면, vector 간의 dot products 값도 더 커지는 경향이 있다. 이러면 softmax 함수의 input이 더 커질 수 있는데,,, 그러면 softmax의 출력이 너무 뾰죡해져서, backpropagation 때 gradients가 매우 작아지는 문제가 생긴다.
우리가 본 이 self-attention function 대신에

attention score들을 루트 d/h로 나누어서 scores들이 더 커지지 않게 막아준다!


2. Residual Connections
이제 optimization trick 몇 가지를 알아보자...!!! 이전 결과와 Layer를 통과한 결과를 더함으로써 그 변화량만 학습한다!!
보통 diagram에서는 종종 Add & Norm이라고 표현되므로 참고하시길..!
Residual Connections은 model 더 잘 traing되도록 도와주는 trick이다.

우리는 보통 i번째 layer의 representaion은 이전 layer의 representation을 layer를 넣은 결과라고 생각한다.

그런데, Residual Connection에서는 위와 같이 바꿔진다. 이전 layer의 representation에 Layer의 representation을 더한다!
즉, 우리는 전체 function를 새로 배우는 게 아니라 residual(변화량)만 학습하면 된다!!
즉 기존 입력 + 변화된 부분을 넣으니 기존 입력을 얼마나 바꿀지를 학습한다.
- 장점
이 구조 덕분에 Gradient가 더 좋아진다. -> 역전파가 잘 전달된다!
Bias도 더 좋아진다!! -> 학습 초기에 입력 그대로 전달하는 함수(identity)에 가까운 편향을 가지게 된다. 모델이 처음엔 뭔가를 바꾸지 않고 그냥 흘려보내는 것에 익숙해짐!

3. Layer normalization
Layer normalizaiton이 model이 더 빠르게 train되도록 도와주는 trick이다.
LayerNorm은 단어 벡터 내부의 값 분포를 정규화해서, 학습을 안정화하고 빠르게 만드는 기법입니다.
- Idea
각 layer에서 hidden vector의 불필요한, 의미없는 variation(잡음)을 cut down하기 위해, standard deviation(표준 편차)과 unit mean을 normalizing하는 것! (평균이 0이고 표준편차가 1이 되도록 정규화하는 것!)
이게 잘 작동하는 이유 중 하나는, gradient(기울기)를 안정적으로 정규화해주기 때문이다.
𝑥 ∈ℝ𝑑 : model에서의 한 individual(word) vector , d차원(embedding 된 차원)임
𝜇 =σ𝑗=1 𝑑 𝑥𝑗 : 이건 mean이에여 𝜇 ∈ ℝ, x의 각 성분을 평균 내면 scala 값이 된다.
𝜎 2 = 1 𝑑 𝑑 σ 𝑗 = 1 𝑥 𝑗 − 𝜇 ; 이건 standard deviation이에여 , 𝜎 ∈ ℝ. 평균에서 얼마나 퍼져 있는지를 측정하면 분산 혹은 표준편차가 된다.
𝛾 ∈ℝ𝑑 : gain parameters 학습 가능한 parameter
𝛽 ∈ℝ𝑑 :bias parameters 학습 가능한 parameter
위의 두 parameter는 최종 출력 scale을 조정하는데 사용, 필요없으면 생략 가능함.
또한 정규화 해주다가 정보 손실의 문제가 있을 수 있으니 복원 가능성을 주기 위해 학습 가능한 파라미터를 붙인다.
그럼녀 layer normalization은 다음과 같이 compute 된다.
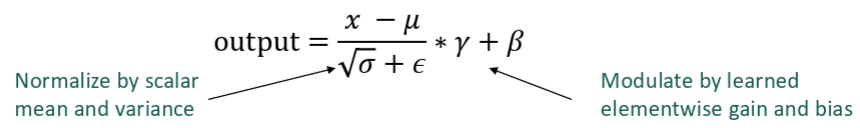
입력 vecotr에서 평균을 빼고 표준편차로 나워서 정규화 한 후 감마와 베타로 scale 조정
짜잔!
Transforemer Decoder는 다음과 같은 Block으로 이루어졌답니다.

- Self-attention
- Add & Norm (이건 각 단계마다 붙여주는 것이라 생각하면 된다)
- Feed-Forward
- Add & Norm
궁금한 것!!
"n × d에서 n은 height고 d는 width처럼 봤는데,
reshape해서 n × h × d/h가 되면 n이 channel이 되는 거야? 아니면 여전히 height야?"
❗️n은 여전히 height (sequence axis), 즉 '단어 수'를 나타내는 축이야.
→ channel 축은 h × d/h 쪽임 (즉, 나중 차원들)
🔸 왜 그렇게 해석해야 하는가?
1. 원래 텐서 구조:
XQ∈Rn×dXQ ∈ ℝ^{n × d}- n: 단어 개수 → 문장 길이 → height (세로)
- d: 각 단어의 임베딩 → width (가로)
이 구조는 마치 이미지에서:
처럼 보임. (2D)
2. reshape:
Rn×h×d/hℝ^{n × h × d/h}- n은 그대로: 단어 수 → 그대로 height (세로)
- h × d/h는: 벡터를 head 수로 분리한 것 → 이게 channel 방향 확장처럼 작동
🔸 이미지와 비교해서 대응시켜보면:
| n | height | 단어 위치 |
| d (or h × d/h) | channel | 임베딩 차원 / attention head |
| (없음) | width | (단어는 1D이므로 가로축 없음) |
✅ 요점 다시 말하면:
- n × d: n은 height처럼 "단어 위치", d는 임베딩 (channel처럼 해석 가능)
- n × h × d/h: n은 여전히 height (단어 위치),
→ h × d/h는 channel dimension처럼 작동 (각 단어당 여러 head 표현)
❗️channel은 맨 뒤쪽 차원이고, height는 항상 단어 순서(n)
reshape를 해도 n이 channel이 되는 건 절대 아님
🔸 감각 비유
이미지에서는:
그래서 문장에서 Token 위치(n) 는 항상 height 역할이지 channel이 아니야.
✅ 요약 정리
| n × d | n × h × d/h | ✅ 여전히 단어 위치 (height) | ✅ h × d/h (뒤쪽이 channel 역할) |
| channel인가? | ❌ 아님 | ❌ |
궁금한 것!!222
matrix의 의미가 고정되어 있는 게 아니라... vision인지, LLM인지 다 다른 거야?"
✅ 맞아. 텐서(행렬)의 각 차원이 뭘 의미하는지는 '도메인'에 따라 달라.
예시: 도메인별 같은 차원이 의미가 다름
| Vision (CNN) | [B, C, H, W] | B: 배치, C: 채널, H: 높이, W: 너비 |
| LLM (Transformer NLP) | [B, N, D] | B: 배치, N: 토큰 수, D: 임베딩 차원 |
| Multi-Head Attention | [B, H, N, D/H] | B: 배치, H: head 수, N: 단어 수, D/H: head당 임베딩 |
| Audio | [B, T, F] | B: 배치, T: 시간축, F: 주파수 bin |
| Time series | [B, T, C] | B: 배치, T: 타임스텝, C: 변수 (채널) |
'AI & ML > LLM' 카테고리의 다른 글
| Pretraining (0) | 2025.07.06 |
|---|---|
| Transformer(1) : Self-attention (0) | 2025.06.21 |
| Attention (0) | 2025.06.21 |
| Machine Translation (MT)의 발전 (0) | 2025.06.21 |
| Language Modeling (0) | 2025.06.21 |